Em estatística, o conceito de variância também pode ser usado para descrever um conjunto de observações. Quando o conjunto das observações é uma população, é chamada de variância da população. Se o conjunto das observações é (apenas) uma amostra estatística, chamamos-lhe de variância amostral (ou variância da amostra).
A variância da população yi onde i = 1, 2, ...., N é dada por
Um método comum de estimar a variância da população é através da tomada de amostras. Quando estimando a variância da população usando n amostras aleatórias xi onde i = 1, 2, ..., n, a fórmula seguinte é um estimador não enviesado:
 é a média da amostra.
é a média da amostra.Notar que o denominador n-1 acima contrasta com a equação para a variância da população. Uma fonte de confusão comum é que o termo variância da amostra e a notação s2 pode referir-se quer ao estimador não enviesado da variância da população acima como também àquilo que é em termos estritos, a variância da amostra, calculada usando n em vez de n-1.
Intuitivamente, o cálculo da variância pela divisão por n em vez de n-1 dá uma subestimativa da variância da população. Isto porque usamos a média da amostra
 como uma estimativa da média da população μ, o que não conhecemos. Na prática, porém, para grandes n, esta distinção é geralmente muito pequena.
como uma estimativa da média da população μ, o que não conhecemos. Na prática, porém, para grandes n, esta distinção é geralmente muito pequena.

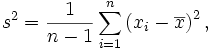
Nenhum comentário:
Postar um comentário