Mediana

A mediana é uma medida de tendência central, um número que caracteriza as observações de uma determinada variável de tal forma que este número (a mediana) de um grupo de dados ordenados separa a metade inferior da amostra, população ou distribuição de probabilidade, da metade superior. Mais concretamente, 1/2 da população terá valores inferiores ou iguais à mediana e 1/2 da população terá valores superiores ou iguais à mediana.
A mediana pode ser calculada para um conjunto de observações ou para funções de distribuição de probabilidade.


Cálculo da mediana para dados ordenados:
No caso de dados ordenados de amostras de tamanho n, se n for ímpar, a mediana será o elemento central . Se n for par, a mediana será o resultado da média simples entre os elementos e .

 Exemplos

Para a seguinte população:
1, 3, 5, 7, 9
A mediana é 5 (igual à média)
No entanto, para a população:
1, 2, 4, 10, 13
A mediana é 4 (enquanto a média é 6)
Para populações pares:
1, 2, 4, 7, 9, 10
A mediana é (4+7)/2, que é 5.5.

Cálculo da mediana para dados classificados

Quando se trata de um conjunto de dados classificados, o cálculo da mediana é feito através do histograma, ou através da função cumulativa de frequências relativas. A mediana é o ponto do eixo das abcissas correspondente a 50% da frequência relativa acumulada.
No caso de variáveis contínuas, a mediana é calculada pela solução da equação ou, equivalentemente, .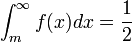
No caso de variáveis discretas, e quando as frequências estão calculadas por unidade, a mediana é o ponto do eixo das abcissas para o qual a frequência relativa acumulada é inferior ou igual a 50% e superior ou igual a 50% para o ponto imediatamente a seguir.