Regressão linear
Em estatística ou Econometria, regressão linear é um método para se estimar a condicional (valor esperado) de uma variável y, dados os valores de algumas outras variáveis x.
A regressão, em geral, trata da questão de se estimar um valor condicional esperado. A regressão linear é chamada "linear" porque se considera que a relação da resposta às variáveis é uma função linear de alguns parâmetros. Os modelos de regressão que não são uma função linear dos parâmetros se chamam modelos de regressão não-linear.
Exemplo de regressão linear.


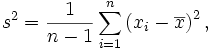
 é a média da amostra.
é a média da amostra.

 . Se n for par, a mediana será o resultado da média simples entre os elementos
. Se n for par, a mediana será o resultado da média simples entre os elementos  e
e  .
. ou, equivalentemente,
ou, equivalentemente, 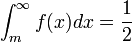 .
.



