Medidas de dispersãoUm aspecto importante no estudo descritivo de um conjunto de dados, é o da determinação da variabilidade ou dispersão desses dados, relativamente à medida de localização do centro da amostra. Supondo ser a média, a medida de localização mais importante, será relativamente a ela que se define a principal medida de dispersão.
Variância Define-se a variância, como sendo a medida que se obtém somando os quadrados dos desvios das observações da amostra, relativamente à sua média, e dividindo pelo número de observações da amostra menos um.
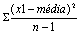
Desvio-padrão
Uma vez que a variância envolve a soma de quadrados, a unidade em que se exprime não é a mesma que a dos dados. Assim, para obter uma medida da variabilidade ou dispersão com as mesmas unidades que os dados, tomamos a raiz quadrada da variância e obtemos o desvio padrão:
O desvio padrão é uma medida que só pode assumir valores não negativos e quanto maior for, maior será a dispersão dos dados.
Algumas propriedades do desvio padrão, que resultam imediatamente da definição, são: o desvio padrão será maior, quanta mais variabilidade houver entre os dados.
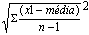


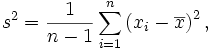
 é a média da amostra.
é a média da amostra.
